Critical Value Calculator
Welcome to our Critical Value Calculator, our ultimate tool for finding critical values for certain statistical tests you can perform (z-test, t-test, χ2-test, F-test and r- test) Designed for students, researchers, and professionals, this calculator will make statistical analysis hassle-free and save you time and effort.
Critical Value Calculator
Result:
How to Calculate Critical Values
One of the easiest ways to calculate critical values is by using our Critical Value Calculator. This user-friendly tool helps you find critical values for various statistical tests, whether two-tailed or one-tailed.
Insert the type of test you are performing. Choose from:
- Z-score
- T-score
- Chi-square (χ²)
- F-score
- Correlation Coefficient (r)
Specify if you are testing a hypothesis with:
- One-tailed test (left-tailed or right-tailed)
- Two-tailed test
- T Critical Value: Enter the significance value (α) and degrees of freedom.
- Z Critical Value: Input the level of significance (α).
- Chi-Square Critical Value: Provide α and degrees of freedom.
- F Critical Value: Enter numerator & denominator degrees of freedom along with α.
- r Critical Value: Specify sample size and value of α.
Click the Calculate button to obtain the critical value relevant to your test. The result will appear instantly!
Related Calculators
Below are more calculators that use critical values to perform statistical analysis.
What are Critical Values?
The critical value, also known as the critical point, is used to decide whether to reject or fail to reject the null hypothesis during hypothesis testing. It is also used to find the lower and upper limits of the confidence interval. Critical values can be left-tailed, right-tailed, or two-tailed.
- Left-Tailed Test: For a left-tailed test, if the test statistic falls to the left of the critical value, we reject the null hypothesis; otherwise, we fail to reject the null hypothesis.
- Right-Tailed Test: For a right-tailed test, if the test statistic falls to the right of the critical value, we reject the null hypothesis; otherwise, we fail to reject the null hypothesis.
- Two-Tailed Test: For a two-tailed test, if the test statistic falls in either the left or right tail beyond the critical value, we reject the null hypothesis; otherwise, we fail to reject the null hypothesis.
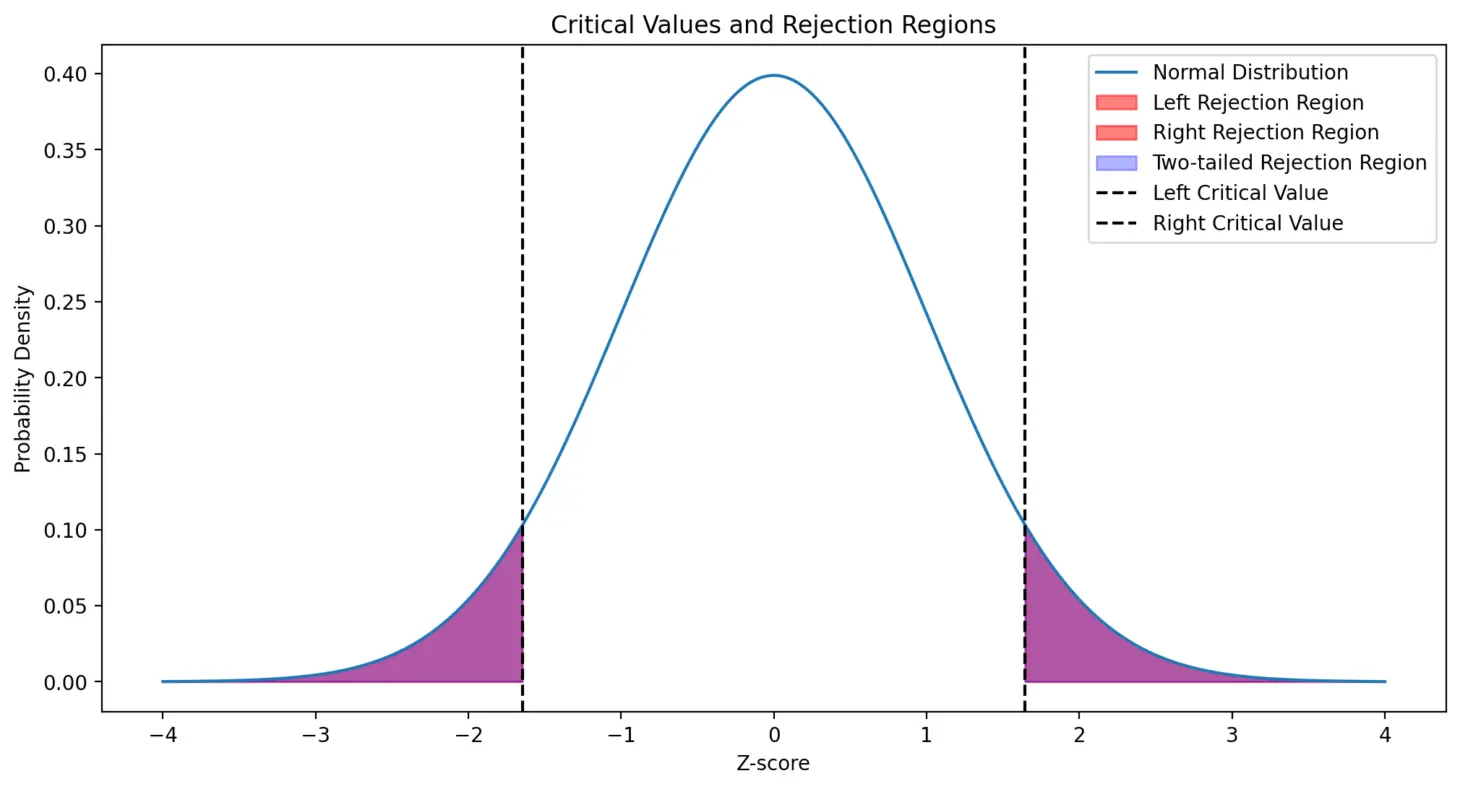
The above figure shows left, right, and two-tailed critical values along with their rejection regions for the z-distribution.
Different Types of Critical Values
T Critical Value
Derived from the t-distribution, used when the sample size is small, or the population standard deviation is unknown. It accounts for the uncertainty of estimating the standard deviation.
- Applications: One-sample/two-sample t-tests, confidence intervals.
- Find: Based on significance level (α), degrees of freedom (DF = n - 1), T-tables, or software.
- Shape: Symmetric and heavy-tailed; approaches the z-distribution as n → ∞.
Z Critical Value
Used when the population standard deviation is known or n > 30, defined by the standard normal distribution.
- Applications: Z-tests for means or proportions, CI with known standard deviation.
- Calculation: Determined by confidence level (α); use z-tables or the formula z = Φ⁻¹(1 − α/2).
- Properties: Symmetric, bell-shaped, and widely used in statistics.
Chi-Square Critical Value
Used for tests with categorical data or variances; depends on degrees of freedom (DF) and significance level (α).
- Applications: Independence tests, goodness-of-fit tests, variance comparisons.
- Calculation: Critical value from chi-square tables or software.
- Shape: Right-skewed; symmetric for large DF.
F Critical Value
Derived from the F-distribution, used to compare variances or test for the significance of a model.
- Applications: ANOVA, regression significance, ratio of variances tests.
- Calculation: Depends on α, numerator DF (df₁), and denominator DF (df₂). Use F-tables or software.
- Shape: Non-negative, right-skewed; skewness decreases with larger DF.
How to Find Value from Table
Critical value tables, such as the Z table, are commonly used to obtain critical values for hypothesis tests. The procedure for finding the critical value is standardized. Below is an example for finding a critical value from the Z table:
Step 1: Selecting the Level of Significance ( α)
- For a two-tailed test, divide α by 2: α = α / 2 .
- For a one-tailed test, use α as is.
Step 2: Determine the Critical Probability
- Left-tailed test: Use the alpha level
directly.
- Right-tailed test: Use 1 - significance
level .
- Two-tailed test: Use both probabilities
above for the respective tails.
Step 3: Find the Value of Interest
- Locate the corresponding Z value on the Z table based on the
calculated probability.
- The Z table provides the cumulative distribution function
(CDF) values, which represent the area to the left of the
Z-score on the standard normal distribution.
Critical Value Tables
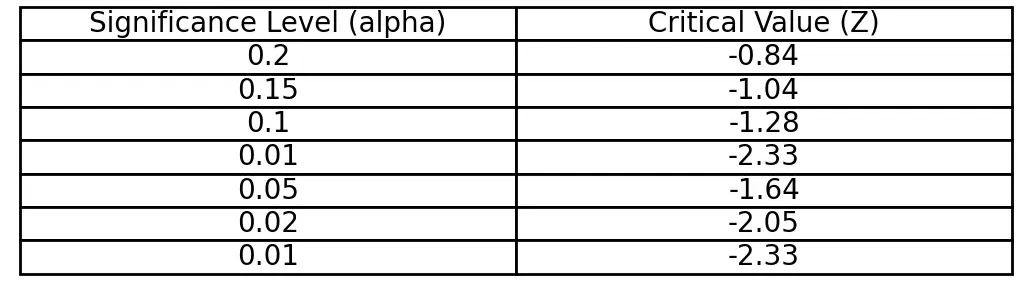
Left-Tailed Critical Value Table for Z Test
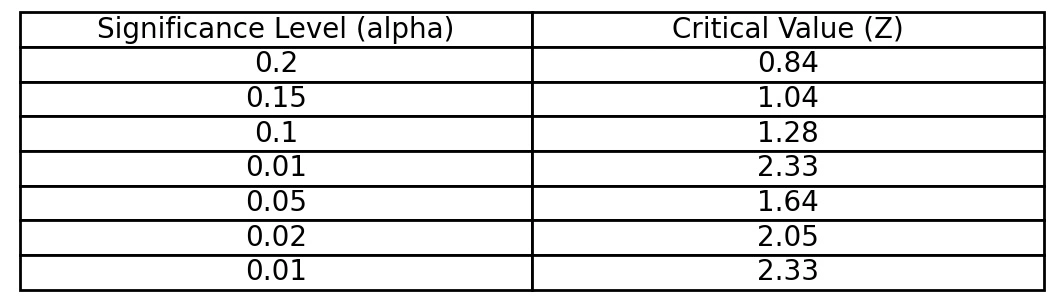
Right-Tailed Critical Value Table for Z Test
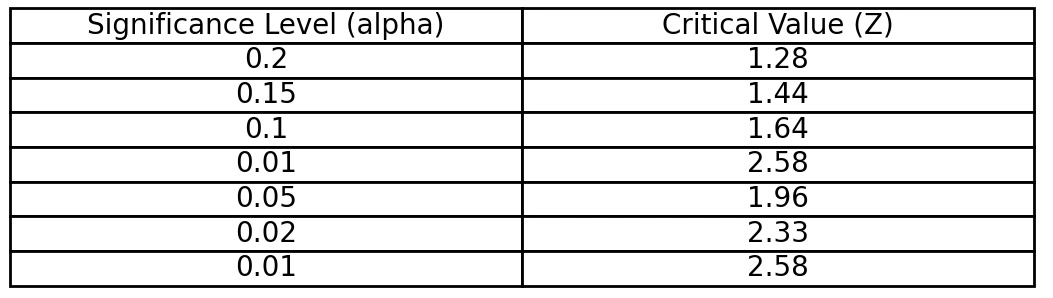
Two-Tailed Critical Value Table for Z Test
Where is Critical Value Used?
Critical values are interpreted across various domains, such as statistical hypothesis testing and research. Below is a breakdown of their applications:
1. Decision Making:
By comparing the critical values with the calculated value of the test statistic (T, Z, r, Chi-Square), critical values help in determining whether to reject or fail to reject the null hypothesis.
2. Significance Levels:
Critical values, typically set at \( \alpha = 0.05 \) or \( \alpha = 0.01 \), assist in understanding how confident you are in the results of the statistical test.
3. Two-Tailed vs. One-Tailed Tests:
Depending on whether the hypothesis test is two-tailed (non-directional hypothesis) or one-tailed (directional hypothesis), different critical values (alpha) are applied.
Practical Examples
In short, critical values are widely applied in various fields such as medical research, market research, and quality control. Below are a few practical applications:
1. Medical Application:
Critical values are used to test the effectiveness of a new drug against a placebo. By comparing test statistics with critical values, researchers determine whether the observed effect is statistically significant.
2. Market Research:
In market research, critical values are used to analyze consumer preferences in paired choice surveys. This helps researchers determine if there is a statistically significant preference for one product over another.
3. Quality Control:
In quality control, critical values are used to determine whether a manufacturing process meets certain specifications. If the test statistic exceeds the critical value, the process is deemed to be outside the acceptable quality range.
FAQs About the Critical Value Calculator
t-critical value: Used for smaller samples or when the population standard deviation is unknown.
Why Use Our Critical Values Calculator?
Precision
Our critical values calculator provides accurate and precise results for various statistical tests, ensuring the reliability of your analysis.
Easy to Use
Designed with a simple and intuitive interface, it allows users to input data easily and obtain results in seconds, even without advanced statistical knowledge.
Multipurpose
Whether you need T, Z, Chi-Square, r, or F critical values, our calculator provides all these computations in a single platform.
Cost-Effective & Accessible
Enjoy free and unlimited online access to our calculator anytime and anywhere, without hidden fees or subscriptions.